chat channel
joafip users mailing list
forums
see
also TreeList of Apache Commons Collections
Like a linked
list but node are linked in a binary tree:
It is a
compromise between list in array and linked list, nearly the same
advantages of linked list in term of memory allocation for append,
but optimize access to element by position for search, append and
delete.
In this way of managing node in tree the node element
value comparison is nether used, node are managed by position on list
point if view of the tree. To make this possible a number of child
information is maintained in each node.
To find the element at a position:
Require to store number of child in each node, it is updated when adding or deleting node:
when adding a node update node number of child from added parent to root path.

when deleting a node update node number of child from deleted parent to root path.

when reorganize for balance using right or left rotation update the number of child of rotated node.
right
rotation
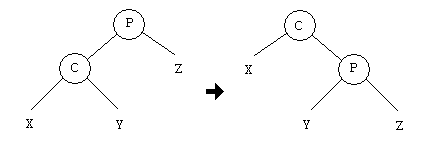
<P number of child> <= <Y number of child> + 1 + <Z number of child> + 1 <C number of child> <= <X number of child> +1 + <P number of child> + 1
left rotation

<P number of child> <= <X number of child> + 1 + <Y number of child> + 1 <C number of child> <= <P number of child> +1 + <Z number of child> + 1
To find the node à position index p, start with current node set to root node and repeat algorithm below until the computed current node position is equals to the position p.
The
root node
position index is the left node number of child + 1
If the
position p is greater than current node position, right of current
node become current node.
If the position p is less than current
node position, left of current node become current node.
The
current node position when go left is <old current
position> -
( <right number of child of new current node> +1 )
-1
The current node position when go right is <old current position> + ( <left number of child of new current node> +1 ) +1
To have the position index of a node.
starting
be
setting current node to node witch for index is searched.
if the
node is a leaf then set index to 0, else set index to <left node
number of child> +1.
while current node have parent, repeat
below:
if
current node is
right child of its parent then add to index <parent left node
number of child> +1.
current node is previous current node
parent.
To insert a node before the position p:
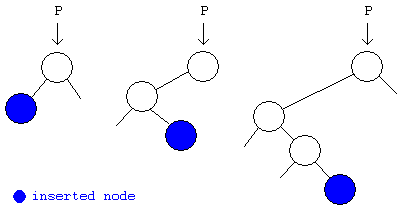
Current
node
is the node at position p.
If current node have not left
child then the parent where insert is current node and node to insert
is left child of its parent.
If current node have not left child
then the parent where insert is the rightest leaf of current
left child and node to insert is right child of its parent.
Then
use the tree reorganize to balance algorithm.
To insert a node after the position p:

Current
node
is the node at position p.
If current node have not right
child then the parent where insert is current node and node to insert
is right child of its parent.
If current node have not right child
then the parent where insert is the leftest leaf of current
right child and node to insert is left child of its parent.
Then
use the tree reorganize to balance algorithm.
To delete a node at position p:
find the node at position p and
then apply the tree delete node algorithm.
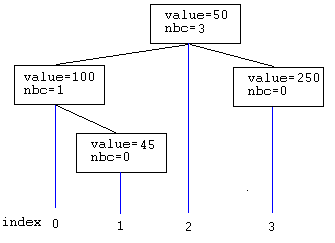
note: nbc is the node
number of
child
Below, the first element of value 100 is added at end of
list ( was empty ). No balancing reorganization needed.

Below, the second element of value 50 is added at end of list. balancing reorganization needed.

below, the third element of value
250 is added at end of list
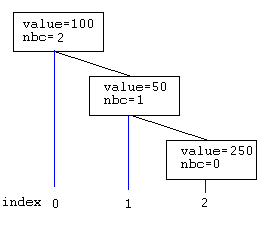
below, the tree is reorganize to
balance it

Below, a fourth element of value 45 is added after element at
position 0. No balancing reorganization needed.